No último artigo escrevi um pouco sobre a história da criptografia, e algumas das formas mais antigas utilizadas para criptografar textos. Uma das mais famosas é a cifra de César, que substitui cada caractere do alfabeto por um caractere diferente.

A cifra de César é considerada simples de quebrar, já que por ser monoalfabética, ou seja, cada caractere é substituído por outro, conseguimos encontrar qual o valor criptografado de cada letra analisando a frequência de caracteres da mensagem. Isso é possível pois o caracter mais utilizado na mensagem criptografada provavelmente deve ser um dos caracteres mais utilizados no idioma da mensagem original.

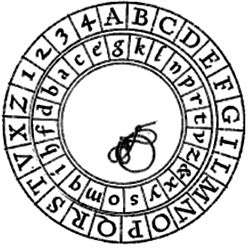
Disco de Alberti

Sabendo da fraqueza deste método de criptografia, vários outros sistemas foram criados. Uma das ferramentas inventadas para auxiliar a codificação de mensagens é o disco de Alberti, criado por Leon Alberti. O disco consiste em duas partes, uma com caracteres externos, que fica parada, e outra com caracteres internos, que pode ser rotacionada. Esse disco é utilizado para criação de cifras polialfabéticas, ou seja, um caractere da mensagem original pode ser substituído por vários outros.

O disco de Alberti pode ser visto na imagem abaixo.

Com esse disco é possível, por exemplo, realizar um alinhamento inicial entre duas letras, e a cada caractere da mensagem a ser codificada rotacionar o disco interno um caractere a direita. Desta forma, a mesma letra na mensagem original pode ter diferentes valores na mensagem criptografada, já que será substituído por diferentes caracteres por conta do movimento do círculo interno. Para conseguir decodificar a mensagem, basta o leitor utilizar o disco com o mesmo alinhamento inicial.

Cifra de Vigenère

Mas esta não foi a única forma de criptografia polialfabética criada. Blaise de Vigenère, um diplomata francês, criou a cifra que é hoje conhecida como cifra de Vigenère.

A cifra de Vigenère consiste em um quadrado de caracteres onde cada linha é uma sequência do alfabeto iniciada por um caractere diferente e uma chave de criptografia utilizada para codificar a mensagem desejada. A chave da criptografia serve para definir quais linhas do quadrado serão utilizadas para codificar a mensagem, e da mesma forma que na cifra de César, os caracteres da mensagem são substituídos por caracteres da linha, utilizando as linhas de acordo com a ordem das letras da palavra chave.

O quadrado de Vigenère é disposto da seguinte forma:

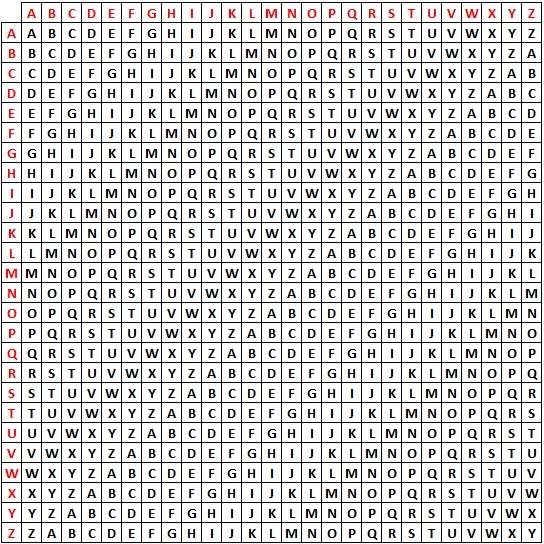
A criptografia de uma mensagem utilizando este quadrado pode seguir da seguinte forma se utilizarmos a cifra ideia para criptografar a mensagem criptografia:

1. Substituímos a primeira letra da mensagem (c) pela terceira letra (já que a letra c é a terceira do alfabeto) da linha que começa pela primeira letra da cifra (neste caso i). Desta forma, a primeira letra da mensagem criptografada ficaria k.
2. Substituímos a segunda letra da mensagem (r) pela decima oitava letra (já que a letra r é a decima oitava do alfabeto) da linha que iniciada pela segunda letra da cifra (neste caso d). Desta forma, a segunda letra da mensagem criptografada ficaria u.
3. Substituímos a terceira letra da mensagem (i) pela nona letra (já que a letra i é a nona do alfabeto) da linha que iniciada pela terceira letra da cifra (neste caso e). Desta forma, a segunda letra da mensagem criptografada ficaria m.
4. Os mesmo passos são feitos para as outras letras da mensagem até o fim das letras da cifra. Ao chegar ao final, volta-se a utilizar do começo as letras da cifra escolhida.

Abaixo você consegue verificar de uma forma interativa como a criptografia funciona.

Cifra

Mensagem

Resultado:

abcdefghijklmnopqrstuvwxyz

bcdefghijklmnopqrstuvwxyza

cdefghijklmnopqrstuvwxyzab

defghijklmnopqrstuvwxyzabc

efghijklmnopqrstuvwxyzabcd

fghijklmnopqrstuvwxyzabcde

ghijklmnopqrstuvwxyzabcdef

hijklmnopqrstuvwxyzabcdefg

ijklmnopqrstuvwxyzabcdefgh

jklmnopqrstuvwxyzabcdefghi

klmnopqrstuvwxyzabcdefghij

lmnopqrstuvwxyzabcdefghijk

mnopqrstuvwxyzabcdefghijkl

nopqrstuvwxyzabcdefghijklm

opqrstuvwxyzabcdefghijklmn

pqrstuvwxyzabcdefghijklmno

qrstuvwxyzabcdefghijklmnop

rstuvwxyzabcdefghijklmnopq

stuvwxyzabcdefghijklmnopqr

tuvwxyzabcdefghijklmnopqrs

uvwxyzabcdefghijklmnopqrst

vwxyzabcdefghijklmnopqrstu

wxyzabcdefghijklmnopqrstuv

xyzabcdefghijklmnopqrstuvw

yzabcdefghijklmnopqrstuvwx

zabcdefghijklmnopqrstuvwxy

Conclusão

Por muito tempo a cifra de Vigenère foi considerada inquebrável por utilizar um modelo polialfabético em que fica muito difícil de decodificar sem saber a palavra chave. Ainda assim, Charles Babbage, um matemático inglês, conseguiu no ano 1854 quebrar essa cifra e decifrar mensagens utilizando um método de frequência e estatística de caracteres.

No livro The Code Book: How to make it, break it, hack it, crack it do Simon Singh, o autor exemplifica passo a passo como é possível quebrar mensagens criptografadas com o cifra de Vigenère. Ele também conta um pouco mais da história de Vigenère e Babbage e quais foram seus objetivos ao criar e quebrar modelos criptográficos.