Bactéria - Experimentos em Programação Criativa

Há alguns anos passei a ter um interesse por programação criativa, e apesar de consumir bastante conteúdo sobre o tema, foram poucas as vezes que de fato implementei algo.

Com várias imagens e gifs de inspiração salvas nesse tempo, quero começar a tentar implementar cada uma dessas ideias. Esses artigos são principalmente criados como uma forma de catalogar o processo de implementação para referencia futura quando eu estiver desenvolvendo novas coisas.

Inspiração

A primeira imagem que tentei replicar através de código é essa:

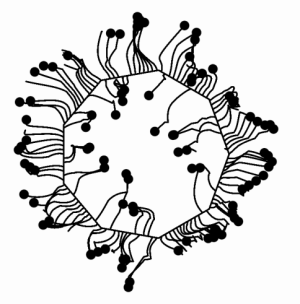
Nonagono com pontos conectando as extremidades

E o meu resultado é o seguinte:

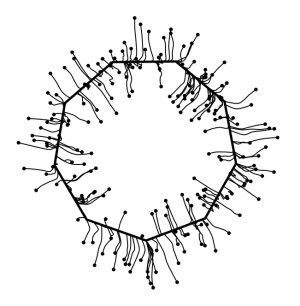
Um parecido nonagono com pontos conectando as extremidades

Implementação

Para implementação dos algoritmos, tenho usado o editor do p5.

Este editor utiliza a própria biblioteca do p5.js, e já conta com um código boilerplate com duas funções: setup, que é disparado antes que qualquer coisa seja desenhada no canvas, e draw que é o loop onde atualizamos o canvas.

1
2
3
4
5
6
7
function setup() {
  createCanvas(400, 400);
}

function draw() {
  background(220);
}

Passo 1

Decidi começar de forma simples, apenas adicionando um polígono no centro da imagem. O p5.js possui algumas funções auxiliares para circulos e quadrados, mas para polígonos o mais fácil é começar adicionando pontos na tela e depois conectá-los.

Como queremos fazer polígonos regulares, onde todos os lados sejam iguais, podemos calcular os pontos com base no seno e coseno de um ângulo, e incrementar esse angulo com base na quantidade de lados

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
function draw() {
  noLoop() // para evitar que a tela atualize muitas vezes
  background(255)
  strokeWeight(5) // grossura dos pontos/linhas
  
  const sides = 8
  const radius = 100
  let angle = 0
  
  for (let i = 0; i < sides; i++) {
    const pointX = radius * sin(angle)
    const pointY = radius * cos(angle)
    
    point(pointX + width/2, pointY + height/2)
    
    angle = angle + TWO_PI / sides
  }
}

Pontos no canvas

Para conectar os pontos, podemos ao invés de usar a função point(x, y), usarmos o vertex(x, y) em conjunto com beginShape() e endShape(CLOSE).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
function draw() {
  noLoop()
  background(255)
  strokeWeight(5)
  noFill() // Para que o polígono não seja preenchido
  
  const vertexes = getPoligonVertexes()
  
  beginShape()
  for (let i = 0; i < vertexes.length; i++) {
    vertex(vertexes[i].x, vertexes[i].y)
  }
  endShape(CLOSE)
}

function getPoligonVertexes(radius = 100, sides = 8) {
  const vertexes = []
  let angle = 0
  
  for (let i = 0; i < sides; i++) {
    const pointX = radius * sin(angle)
    const pointY = radius * cos(angle)
    
    const vector = createVector(pointX + width / 2, pointY + height / 2)
    vertexes.push(vector)
    
    angle = angle + TWO_PI / sides
  }

  return vertexes
}

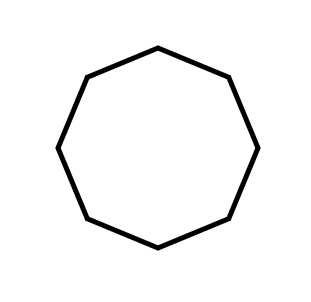
Polígono completo

Passo 2

O próximo passo foi adicionar os tentáculos saindo do polígono. Pensei em duas formas que isso poderia ser feito: 1. selecionar pontos aleatórios ao redor do polígono e conectá-los à extremidade mais próxima, ou 2. selecionar pontos aleatórios nas extremidades e caminhar até algum ponto mais distante.

Em minha implementação escolhei a primeira opção. Para isso criei uma função que gera pontos a partir de um ângulo aleatório, e posiciono ele em um raio próximo ao raio de nosso polígono.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
function draw() {
  ...

  const dots = getDots()
  
  for (let i = 0; i < dots.length; i++) {
    point(dots[i].x, dots[i].y)
  }
}

function getDots(count = 100) {
  const minRadius = width / 5
  const maxRadius = width / 3
  const dots = []
  for (let i = 0; i < count; i++) {
    const angle = Math.random() * TWO_PI
    const x = Math.cos(angle) * random(minRadius, maxRadius) + width / 2
    const y = Math.sin(angle) * random(minRadius, maxRadius) + height / 2

    const vector = createVector(x, y)
    dots.push(vector)
  }
  return dots
}

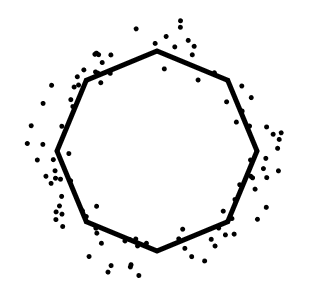
Polígono e pontos

Para conectar esses pontos ao polígono pedi ajuda para o ChatGPT. Aparentemente a forma mais simples é encontrar o ponto de menor distância entre um vértice e um segmento de linha, e fazer isso para todas as arestas de um polígono. Assim conseguimos encontrar qual o ponto mais próximo do vértice e do polígono. O próprio ChatGPT me ajudou criando o código para essa etapa:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
function getClosestPolygonVertex(vertex, polygonVertexes = []) {
  let closest
  let closestDistance = Infinity

  for (let i = 0; i < polygonVertexes.length; i++) {
    // Loop entre os vertices do polígonos, pegando o atual e o seguinte, que formam a linha
    const isLast = (i+1) === polygonVertexes.length
    const v1 = polygonVertexes[i]
    const v2 = polygonVertexes[isLast ? 0 : i+1]
    
    const closestPoint = getClosestPointFromVertexToLine(vertex, v1, v2)
    const distance = distanceFromVertexes(vertex, closestPoint)
    
    if (distance < closestDistance) {
      closestDistance = distance
      closest = closestPoint
    }
  }
  
  return closest
}

function getClosestPointFromVertexToLine(vertex, lineStart, lineEnd) {
  // Calculate the vector representing the line segment
  const lineSegmentVector = createVector(lineEnd.x - lineStart.x, lineEnd.y - lineStart.y)
  
  // Calculate the vector from the line segment start to the vertex
  const vertexVector = createVector(vertex.x - lineStart.x, vertex.y - lineStart.y)

  // Calculate the dot product of the line segment vector and the vertex vector
  const dotProduct = lineSegmentVector.x * vertexVector.x + lineSegmentVector.y * vertexVector.y;

  // Calculate the squared length of the line segment vector
  const squaredLength = lineSegmentVector.x * lineSegmentVector.x + lineSegmentVector.y * lineSegmentVector.y;

  // Calculate the parameter value of the closest point on the line segment to the vertex
  const t = Math.max(0, Math.min(1, dotProduct / squaredLength));

  // Calculate the coordinates of the closest point on the line segment
  const closestPoint = createVector(lineStart.x + t * lineSegmentVector.x, lineStart.y + t * lineSegmentVector.y)

  return closestPoint
}

function distanceFromVertexes(vertex1, vertex2) {
  return Math.sqrt(
    (vertex1.x - vertex2.x) * (vertex1.x - vertex2.x) +
    (vertex1.y - vertex2.y) * (vertex1.y - vertex2.y)
  )
}

Com essas funções, podemos atualizar o método draw para desenhar a linha entre os pontos e o polígono:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
function draw() {
  ...
  
  const dots = getDots()

  for (let i = 0; i < dots.length; i++) {
    // Desenhando o ponto
    strokeWeight(10)
    point(dots[i].x, dots[i].y)

    // Desenhando a linha
    strokeWeight(2) // Alterando a largura entre o ponto e a linha
    beginShape()
    vertex(dots[i].x, dots[i].y)
    const closestPolygonVertex = getClosestPolygonVertex(dots[i], vertexes)
    vertex(closestPolygonVertex.x, closestPolygonVertex.y)
    endShape(CLOSE) 
  }
}

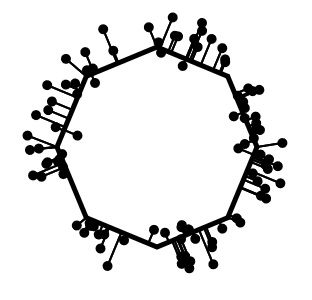
Polígono e pontos conectados

Passo 3

O terceiro e último passo de minha implementação foi deixas os tentáculos curvados, ao invés de simples linhas retas. Para isso, uma forma fácil é segmentar a reta em n pontos e movê-los de forma aleatória para uma direção próxima.

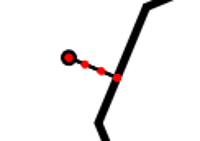
Segmentos do tentáculo
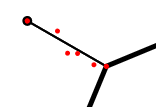
Segmentos do tentáculo com movimento

Para segmentar a linha, pedi uma nova ajuda ao ChatGPT:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
function segmentizeLine(lineSegmentStart, lineSegmentEnd, segmentCount = 10) {
  const points = [];
  const dx = (lineSegmentEnd.x - lineSegmentStart.x) / (segmentCount - 1);
  const dy = (lineSegmentEnd.y - lineSegmentStart.y) / (segmentCount - 1);

  for (let i = 0; i < segmentCount; i++) {
    let x = lineSegmentStart.x + dx * i;
    let y = lineSegmentStart.y + dy * i;

    points.push({ x, y });
  }

  return points;
}

Fiz uma leve alteração para mover os segmentos centrais:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

function segmentizeLine(lineSegmentStart, lineSegmentEnd, segmentCount = 10) {
  const points = [];
  const dx = (lineSegmentEnd.x - lineSegmentStart.x) / (segmentCount - 1);
  const dy = (lineSegmentEnd.y - lineSegmentStart.y) / (segmentCount - 1);

  for (let i = 0; i < segmentCount; i++) {
    let x = lineSegmentStart.x + dx * i;
    let y = lineSegmentStart.y + dy * i;

    // Não queremos mover a posição do primeiro vértice e do vértice que encosta no polígono
    if (i > 0 && i < segmentCount-1) {
      x += random(0, 15)
      y += random(0, 15)
    }
    
    // Para utilizar a função `curveVertex` precisamos do primeiro e último vértices duplicados
    if (i === 0 || i === segmentCount-1) {
      points.push(createVector(x, y));  
    }
    
    points.push(createVector(x, y));
  }

  return points;
}

E utilizando essa função junto com o curveVertex, conseguimos ter os tentáculos curvos:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
function draw() {
  ...
  
  const dots = getDots()

  for (let i = 0; i < dots.length; i++) {
    stroke('black')
    strokeWeight(10)
    point(dots[i].x, dots[i].y)

    // Desenhando a linha
    strokeWeight(2) // Alterando a largura entre o ponto e a linha
    const closestPolygonVertex = getClosestPolygonVertex(dots[i], vertexes)
    const segments = segmentizeLine(dots[i], closestPolygonVertex, 6)
    beginShape()
    for (let j = 0; j < segments.length; j++) {
      curveVertex(segments[j].x, segments[j].y)
    }
    endShape() 
  }
}

Assim tempos o resultado final:

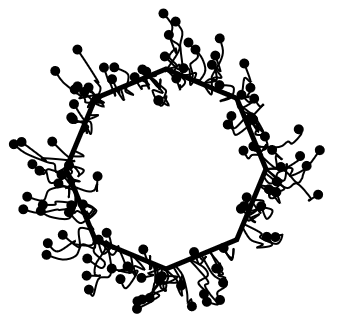
Resultado final

Próximos passos

Para chegar mais próximo do original, algumas possível mudanças seriam:

  • Alterar a forma como adicionamos aleatóriedade nos segmentos do tentáculo para ficarem menos distantes, talvez utilizando noise ao invés de random
  • Alterar a aleatóriedade dos pontos para que não sejam gerados pontos tão próximos do polígono

Por mais que ainda possa ser melhorado, fiquei satisfeito com esse resultado e empolgado para começar um próximo.

Código completo 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
function setup() {
  createCanvas(400, 400)
}

function draw() {
  noLoop()
  background(255)
  strokeWeight(5)
  noFill() // Para que o polígono não seja preenchido
  
  const vertexes = getPoligonVertexes()
  
  beginShape()
  for (let i = 0; i < vertexes.length; i++) {
    vertex(vertexes[i].x, vertexes[i].y)
  }
  endShape(CLOSE)
  
  const dots = getDots()

  for (let i = 0; i < dots.length; i++) {
    stroke('black')
    strokeWeight(10)
    point(dots[i].x, dots[i].y)

    // Desenhando a linha
    strokeWeight(2) // Alterando a largura entre o ponto e a linha
    const closestPolygonVertex = getClosestPolygonVertex(dots[i], vertexes)
    const segments = segmentizeLine(dots[i], closestPolygonVertex, 6)
    beginShape()
    for (let j = 0; j < segments.length; j++) {
      curveVertex(segments[j].x, segments[j].y)
    }
    endShape() 
  }
}

function getPoligonVertexes(radius = 100, sides = 8) {
  const vertexes = []
  let angle = 0
  
  for (let i = 0; i < sides; i++) {
    const pointX = radius * sin(angle)
    const pointY = radius * cos(angle)
    
    const vector = createVector(pointX + width/2, pointY + height/2)
    vertexes.push(vector)
    
    angle = angle + TWO_PI / sides
  }

  return vertexes
}

function getDots(count = 100) {
  const minRadius = width / 6
  const maxRadius = width / 2.5
  const dots = []
  for (let i = 0; i < count; i++) {
    const angle = Math.random() * TWO_PI
    const x = Math.cos(angle) * random(minRadius, maxRadius) + width / 2
    const y = Math.sin(angle) * random(minRadius, maxRadius) + height / 2

    const vector = createVector(x, y)
    dots.push(vector)
  }
  return dots
}

function getClosestPolygonVertex(vertex, polygonVertexes = []) {
  let closest
  let closestDistance = Infinity

  for (let i = 0; i < polygonVertexes.length; i++) {
    // Loop entre os vertices do polígonos, pegando o atual e o seguinte, que formam a linha
    const isLast = (i+1) === polygonVertexes.length
    const v1 = polygonVertexes[i]
    const v2 = polygonVertexes[isLast ? 0 : i+1]
    
    const closestPoint = getClosestPointFromVertexToLine(vertex, v1, v2)
    const distance = distanceFromVertexes(vertex, closestPoint)
    
    if (distance < closestDistance) {
      closestDistance = distance
      closest = closestPoint
    }
  }
  
  return closest
}

function getClosestPointFromVertexToLine(vertex, lineStart, lineEnd) {
  // Calculate the vector representing the line segment
  const lineSegmentVector = createVector(lineEnd.x - lineStart.x, lineEnd.y - lineStart.y)
  
  // Calculate the vector from the line segment start to the vertex
  const vertexVector = createVector(vertex.x - lineStart.x, vertex.y - lineStart.y)

  // Calculate the dot product of the line segment vector and the vertex vector
  const dotProduct = lineSegmentVector.x * vertexVector.x + lineSegmentVector.y * vertexVector.y;

  // Calculate the squared length of the line segment vector
  const squaredLength = lineSegmentVector.x * lineSegmentVector.x + lineSegmentVector.y * lineSegmentVector.y;

  // Calculate the parameter value of the closest point on the line segment to the vertex
  const t = Math.max(0, Math.min(1, dotProduct / squaredLength));

  // Calculate the coordinates of the closest point on the line segment
  const closestPoint = createVector(lineStart.x + t * lineSegmentVector.x, lineStart.y + t * lineSegmentVector.y)

  return closestPoint
}

function distanceFromVertexes(vertex1, vertex2) {
  return Math.sqrt(
    (vertex1.x - vertex2.x) * (vertex1.x - vertex2.x) +
    (vertex1.y - vertex2.y) * (vertex1.y - vertex2.y)
  )
}

function segmentizeLine(lineSegmentStart, lineSegmentEnd, segmentCount = 10) {
  const points = [];
  const dx = (lineSegmentEnd.x - lineSegmentStart.x) / (segmentCount - 1);
  const dy = (lineSegmentEnd.y - lineSegmentStart.y) / (segmentCount - 1);

  for (let i = 0; i < segmentCount; i++) {
    let x = lineSegmentStart.x + dx * i;
    let y = lineSegmentStart.y + dy * i;

    // Não queremos mover a posição do primeiro vértice e do vértice que encosta no polígono
    if (i > 0 && i < segmentCount-1) {
      x += random(0, 15)
      y += random(0, 15)
    }
    
    // Para utilizar a função `curveVertex` precisamos do primeiro e último vértices duplicados
    if (i === 0 || i === segmentCount-1) {
      points.push(createVector(x, y));  
    }
    
    points.push(createVector(x, y));
  }

  return points;
}

Post Anterior
Post Seguinte