Hexagonos - Experimentos em Programação Criativa - 11

Essa é mais uma tentativa de reproduzir uma imagem utilizando computação criativa. Como nas últimas vezes, o objetivo dessa tentativa é de utilizar uma inspiração para aprender técnicas e conceitos novos. Esses artigos são principalmente criados como uma forma de catalogar o processo de implementação para referencia futura quando eu estiver desenvolvendo novas coisas.

Inspiração

Desta vez, uma das imagens que eu tinha salvo como inspiração é a seguinte:

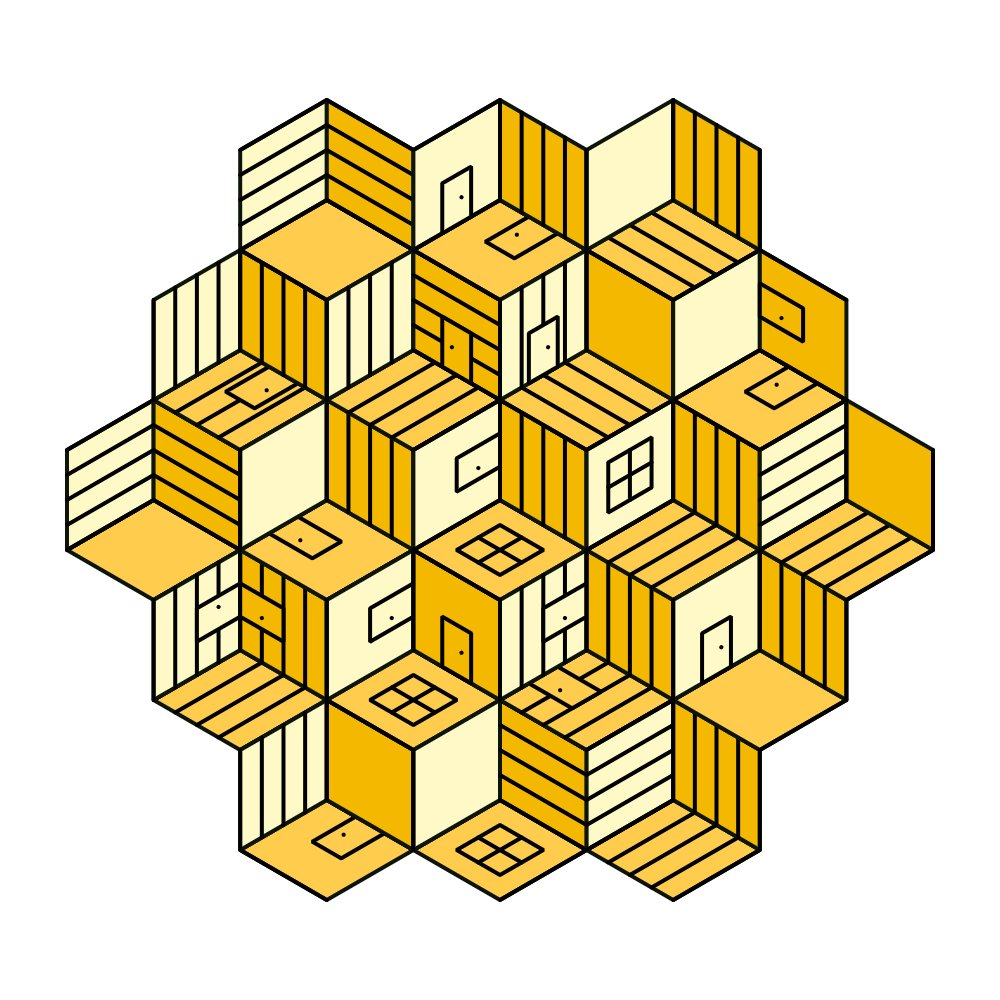
Múltiplos hexagonos parecendo salas

No caso dessa imagem, lembrei que tinha encontrado através do canal Birb’s Nest no discord, então fui atrás da origem. Não encontrei a exata imagem, mas encontrei esse ótimo artigo do Gorilla Sun, e esse projeto de Roni Kaufman no Open Processing, que por sinal é o mesmo autor da imagem de inspiração.

Implementação

Usarei novamento o editor do p5 para essa implementação.

Neste artigo, diferentemente dos outros dessa série, vou analisar e alterar o projeto acima para tentar chegar no resultado da imagem de inspiração. Isso irá facilitar chegar no resultado, e é algo que geralmente faço em outros projetos (alterar códigos prontos para chegar em novos resultados)

Passo 1

O código completo do projeto de Roni Kaufman pode ser visto abaixo, assim como o resultado, mas vamos analisá-lo passo a passo

Código completo 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
const matrix = []

const WIDTH = 60
const CHECKED_SIZE = 6

function setup() {
  createCanvas(WIDTH * (CHECKED_SIZE + 2), WIDTH * (CHECKED_SIZE + 2))
  
  new Array(CHECKED_SIZE).fill(0).map((_, i) => {
    matrix.push([])
    new Array(CHECKED_SIZE).fill(0).map((_, j) => {
      const v = i % 2 === 0 ? (j % 2 === 0 ? 1 : 0) : (j % 2 === 0 ? 0 : 1)
      matrix[i].push(v)
    })
  })
}

function draw() {
  background(220)
  stroke(0)
  strokeWeight(2)
  
  for (let i = 0; i < matrix.length; i++) {
    for (let j = 0; j < matrix[i].length; j++) {
      fill(matrix[i][j] === 1 ? 0 : 220)
      const x = WIDTH * i + WIDTH
      const y = WIDTH * j + WIDTH
      square(x, y, WIDTH)
      
      const isXWall = i === 0 || i === CHECKED_SIZE - 1
      const isYWall = j === 0 || j === CHECKED_SIZE - 1
      if (isXWall && isYWall) {
        fill(matrix[i][j] === 1 ? 220 : 0)
        circle(x + WIDTH/2, y + WIDTH/2, WIDTH / 2)
      }
    }
  }
}

function mouseClicked() {
  const isLeftWall = mouseX < WIDTH
  const isRightWall = mouseX > WIDTH * 7
  const isTopWall = mouseY < WIDTH
  const isBottomWall = mouseY > WIDTH * 7
  if (isLeftWall || isRightWall) {
    const row = floor(mouseY * (CHECKED_SIZE + 2) / width)
    rotateMatrix(row - 1, 'x', isLeftWall ? 'right' : 'left')
  }
  if (isTopWall || isBottomWall) {
    const column = floor(mouseX * (CHECKED_SIZE + 2) / width)
    rotateMatrix(column - 1, 'y', isTopWall ? 'bottom' : 'top')
  }
}

function rotateMatrix(index, axis, direction) {
  if (index < 0 || index >= CHECKED_SIZE) return
  if(axis === 'y') {
    if (direction === 'bottom') {
      matrix[index].unshift(matrix[index].pop())
    } else {
      matrix[index].push(matrix[index].shift())
    }
  } else {
    const cells = matrix.map(row => row[index])
    if (direction === 'right') {
      cells.unshift(cells.pop())
    } else {
      cells.push(cells.shift())
    }
    matrix.forEach((row, i) => row[index] = cells[i])
  }
}

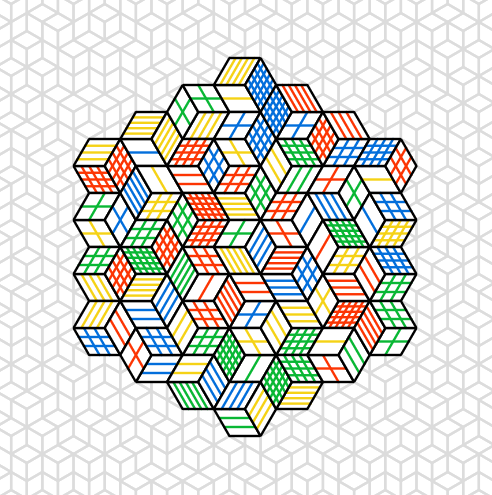
Múltiplos hexagonos listrados

No setup da aplicação, podemos ver que algumas cores são definidas (provavelmente as cores das linhas internas de cada hexagono), além de algumas configurações básicas para as linhas. Podemos ver também que ele não será executado em um loop. Para chegarmos no resultado que buscamos vamos precisar mudar as cores.

1
2
3
4
5
6
7
8
9
10
const SQRT3 = Math.sqrt(3);
let colors = ["#026edb", "#f5d216", "#fc3503", "#09b734"];

function setup() {
  createCanvas(496, 496);
  noLoop();
  strokeWeight(2.4);
  strokeJoin(BEVEL);
  noFill();
}

O método de desenho, por sua vez, possui alguns loops. Vendo o resultado renderizado em tela, posso presumir que um dos loops irá desenhar o plano de fundo, e o outro os hexagonos acima.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
function draw() {
  translate(width/2, height/2);
  rotate(random(([0, PI/6])));
  background(255);
  
  let s = 18;
  let t = s*SQRT3;
  stroke(220);
  let n = 13;
  for (let i = -n; i <= n; i++) {
    for (let j = -n; j <= n; j++) {
      let x = (i*SQRT3 + j*SQRT3/2)*s;
      let y = (j*3/2)*s;
      let theta0 = random([0, PI/3]);
      for (let theta = theta0+PI/6; theta < TWO_PI; theta += TWO_PI/3) {
        push();
        translate(x + cos(theta)*s/2, y + sin(theta)*s/2);
        rotate(theta+PI/2);
        makeRhombus(s, t);
        pop();
      }
    }
  }
  
  rotate(PI/6);  
  s *= SQRT3;
  t *= SQRT3;
  n = 7;
  for (let i = -n; i <= n; i++) {
    for (let j = -n; j <= n; j++) {
      let x = (i*SQRT3 + j*SQRT3/2)*s;
      let y = (j*3/2)*s;
      if (dist(x, y, 0, 0) < 185) {
        let mode = random([0, 1]); // which orientation for the hexagon
        let theta0 = (mode == 0) ? 0 : PI/3;
        for (let theta = theta0+PI/6; theta < TWO_PI; theta += TWO_PI/3) {
          push();
          translate(x + cos(theta)*s/2, y + sin(theta)*s/2);
          rotate(theta+PI/2);
          let l = floor(random(2, 6));
          noStroke();
          fill(255);
          makeRhombus(s, t);
          stroke(random(colors));
          makeRhombusLines(s, t, l);
          stroke(0);
          noFill();
          makeRhombus(s, t);
          pop();
        }
      }
    }
  }
}

Por fim temos algumas funções auxiliares criando “rhombus”, ou losangos, e o que parecem ser suas linhas iternas. Por isso podemos presumir que não são necessáriamente hexagonos desenhados, mas sim 3 losangos lado a lado formando cada hexagono.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
function makeRhombus(s, t) {
  beginShape();
  vertex(0, -s/2);
  vertex(t/2, 0);
  vertex(0, s/2);
  vertex(-t/2, 0);
  endShape(CLOSE);
}

function makeRhombusLines(s, t, l) {
  let a = [0, -s/2]; // top vertex
  let b = [t/2, 0]; // right vertex
  let c = [0, s/2]; // bottom vertex
  let d = [-t/2, 0]; // left vertex
  
  if (random() < 1/2) {
    [b, d] = [d, b];
  }
  
  let double = random() < 1/2;
  
  for (let z = 1/l; z < 1; z += 1/l) {
    let [x1, y1] = prop(a, b, z);
    let [x2, y2] = prop(d, c, z);
    line(x1, y1, x2, y2);
    if (double) {
      [x1, y1] = prop(a, d, z);
      [x2, y2] = prop(b, c, z);
      line(x1, y1, x2, y2);
    }
  }
}
  
function prop(a, b, k) {
  let xC = (1-k)*a[0] + k*b[0];
  let yC = (1-k)*a[1] + k*b[1];
  return [xC, yC];
}

Passo 2

Começando de forma fácil, vamos remover o primeiro loop da função de desenho, e alterar um pouco os valores para descobrir a função de cada um.
De cara, podemos descobrir, aumentando e diminuindo o valor da const s, que esse aparenta ser o tamanho dos losangos. Vamos então aumentá-lo para 40, e remover o acrécimo que é feito a ele antes do segundo loop, ficando assim mais próximo da imagem de inspiração.

Múltiplos hexagonos listrados

Outra coisa que podemos notar é a const mode, que define a direção dos hexagonos. Vamos removê-la, removendo também a const theta0, pois não vamos usar esses diferentes modos. Além disso, remover as funções de rotate e ajustar o size

A função de desenho ficou assim após essas alterações:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
function draw() {
  translate(width/2, height/2);
  background(255);
  
  let size = 40;
  let t = size*SQRT3;
  stroke(220);
  
  let n = 7;
  for (let i = -n; i <= n; i++) {
    for (let j = -n; j <= n; j++) {
      let x = (i*SQRT3 + j*SQRT3/2)*size;
      let y = (j*3/2)*size;
      if (dist(x, y, 0, 0) < 175) {
        for (let theta = PI/6; theta < TWO_PI; theta += TWO_PI/3) {
          push();
          translate(x + cos(theta)*size/2, y + sin(theta)*size/2);
          rotate(theta+PI/2);
          let l = floor(random(2, 6));
          noStroke();
          fill(255);
          makeRhombus(size, t);
          stroke(random(colors));
          makeRhombusLines(size, t, l);
          stroke(0);
          noFill();
          makeRhombus(size, t);
          pop();
        }
      }
    }
  }
}

Passo 3

Vamos agora ajustar as cores. Dentro do loop podemos ver que as cores das linhas são definidas com a função stroke(random(colors));. Vamos mudá-la para apenas stroke(0);.
Para os amarelos, podemos trocar o fill(255);, por uma validação na váriavel theta do loop, onde pegamos o resto da divisão do valor por 3 (cada lado) e adicionamos uma cor para cada lado:

1
2
3
if(floor(theta)%3 === 0) fill(255,250,193);
if(floor(theta)%3 === 1) fill(252,179,0);
if(floor(theta)%3 === 2) fill(255,203,31);

A função de desenho atualizada fica assim:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
function draw() {
  translate(width/2, height/2);
  background(255);
  
  let size = 40;
  let t = size*SQRT3;
  stroke(220);
  
  let n = 7;
  for (let i = -n; i <= n; i++) {
    for (let j = -n; j <= n; j++) {
      let x = (i*SQRT3 + j*SQRT3/2)*size;
      let y = (j*3/2)*size;
      if (dist(x, y, 0, 0) < 175) {
        for (let theta = PI/6; theta < TWO_PI; theta += TWO_PI/3) {
          push();
          translate(x + cos(theta)*size/2, y + sin(theta)*size/2);
          rotate(theta+PI/2);
          let l = floor(random(2, 6));
          noStroke();
          if(floor(theta)%3 === 0) fill(255,250,193);
          if(floor(theta)%3 === 1) fill(252,179,0);
          if(floor(theta)%3 === 2) fill(255,203,31);
          makeRhombus(size, t);
          stroke(0);
          makeRhombusLines(size, t, l);
          stroke(0);
          noFill();
          makeRhombus(size, t);
          pop();
        }
      }
    }
  }
}

E esse é o resultado

Múltiplos hexagonos amarelos listrados

Passo 4

Para a próxima parte, vamos alterar a função que altera as linhas dos losangos. Para facilitar, vou criar uma função para cada tipo de parede, e chamálas de forma aleatória dentro da função makeRhombusLines(s, t) já existente:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
function makeRhombusLines(s, t) {
  let a = [0, -s/2]; // top vertex
  let b = [t/2, 0]; // right vertex
  let c = [0, s/2]; // bottom vertex
  let d = [-t/2, 0]; // left vertex
  
  // Invert direction of inner content on same side of hexagon
  if (random() < 1/2) {
    [b, d] = [d, b];
  }
  
  const isStripped = round(random(1,2)) === 1
  const type = round(random(1,8))
  if (isStripped) makeStripedWall(a,b,c,d)
  if (type === 2) makeDoor(s,t)
  if (!isStripped && type === 3) makeWindow(s,t)
}

function makeStripedWall(a,b,c,d) {
}
  
function makeDoor(s,t) {
}

function makeWindow(s,t) {
}

Para a função de parede listrada será fácil. Basta usarmos a mesma que já tinhamos originalmente. A única diferença é que não iremos pintar duas vezes fazendo xadrezes.

1
2
3
4
5
6
7
function makeStripedWall(a,b,c,d) {
  for (let z = 1/4; z < 1; z += 1/4) {
    let [x1, y1] = prop(a, b, z);
    let [x2, y2] = prop(d, c, z);
    line(x1, y1, x2, y2);
  }
}

A função de janela também é simples. Podemos usar a mesma lógica de fazer os hexagonos e o xadrez, porém reduzindo o tamanho e usando apenas uma linha vertical e horizontal.

1
2
3
4
5
6
7
8
9
10
11
12
13
function makeWindow(s,t) {
  makeRhombus(s/2,t/2)
  let a = [0, -s/4]; // top vertex
  let b = [t/4, 0]; // right vertex
  let c = [0, s/4]; // bottom vertex
  let d = [-t/4, 0]; // left vertex
  let [vx1, vy1] = prop(a, b, 1/2);
  let [vx2, vy2] = prop(d, c, 1/2);
  line(vx1,vy1,vx2,vy2)
  let [hx1, hy1] = prop(a, d, 1/2);
  let [hx2, hy2] = prop(b, c, 1/2);
  line(hx1,hy1,hx2,hy2)
}

Para a porta, decidi fazer apenas um losango e movê-lo para o canto do losango maior, e adicionar um ponto. A lógica fica bem simples, por mais que não fique exatamente igual à imagem de inspiração.

1
2
3
4
5
6
7
8
function makeDoor(s,t) {
  push();
  translate(-t/8, -s/8)
  makeRhombus(s/2,t/2)
  
  point(t/16, -s/12);
  pop();
}

Múltiplos hexagonos amarelos listrados e com janelas

Próximos passos

Esse artigo foi um dos mais simples de implementar, já que todo o trabalho duro foi copiado do projeto original de Roni Kaufman. De qualquer forma, acho um bom exercício modificar projetos de outros programadores, pois assim aprendemos coisas novas e novas formas de implementar pequenos algoritmos.

Para terminar esse projeto com um visual mais similar ao da imagem de inspiração, ajustar a largura da porta seria o último passo.

Código completo 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
const SQRT3 = Math.sqrt(3);

function setup() {
  createCanvas(496, 496);
  noLoop();
  strokeWeight(2.4);
  strokeJoin(BEVEL);
  noFill();
}

function draw() {
  translate(width/2, height/2);
  background(255);
  
  let size = 40;
  let t = size*SQRT3;
  stroke(220);
  
  let n = 7;
  for (let i = -n; i <= n; i++) {
    for (let j = -n; j <= n; j++) {
      let x = (i*SQRT3 + j*SQRT3/2)*size;
      let y = (j*3/2)*size;
      if (dist(x, y, 0, 0) < 175) {
        for (let theta = PI/6; theta < TWO_PI; theta += TWO_PI/3) {
          push();
          translate(x + cos(theta)*size/2, y + sin(theta)*size/2);
          rotate(theta+PI/2);
          let l = floor(random(2, 6));
          noStroke();
          if(floor(theta)%3 === 0) fill(255,250,193);
          if(floor(theta)%3 === 1) fill(252,179,0);
          if(floor(theta)%3 === 2) fill(255,203,31);
          makeRhombus(size, t);
          stroke(0);
          makeRhombusLines(size, t, l);
          stroke(0);
          noFill();
          makeRhombus(size, t);
          pop();
        }
      }
    }
  }
}

function makeRhombus(s, t) {
  beginShape();
  vertex(0, -s/2);
  vertex(t/2, 0);
  vertex(0, s/2);
  vertex(-t/2, 0);
  endShape(CLOSE);
}

function makeRhombusLines(s, t) {
  let a = [0, -s/2]; // top vertex
  let b = [t/2, 0]; // right vertex
  let c = [0, s/2]; // bottom vertex
  let d = [-t/2, 0]; // left vertex
  
  // Invert direction of inner content on same side of hexagon
  if (random() < 1/2) {
    [b, d] = [d, b];
  }
  
  const isStripped = round(random(1,2)) === 1
  const type = round(random(1,8))
  if (isStripped) makeStripedWall(a,b,c,d)
  if (type === 2) makeDoor(s,t)
  if (!isStripped && type === 3) makeWindow(s,t)
}

function makeStripedWall(a,b,c,d) {
  for (let z = 1/4; z < 1; z += 1/4) {
    let [x1, y1] = prop(a, b, z);
    let [x2, y2] = prop(d, c, z);
    line(x1, y1, x2, y2);
  }
}

function makeWindow(s,t) {
  makeRhombus(s/2,t/2)
  let a = [0, -s/4]; // top vertex
  let b = [t/4, 0]; // right vertex
  let c = [0, s/4]; // bottom vertex
  let d = [-t/4, 0]; // left vertex
  let [vx1, vy1] = prop(a, b, 1/2);
  let [vx2, vy2] = prop(d, c, 1/2);
  line(vx1,vy1,vx2,vy2)
  let [hx1, hy1] = prop(a, d, 1/2);
  let [hx2, hy2] = prop(b, c, 1/2);
  line(hx1,hy1,hx2,hy2)
}
  
function makeDoor(s,t) {
  push();
  translate(-t/8, -s/8)
  makeRhombus(s/2,t/2)
  
  point(t/16, -s/12);
  pop();
}

function prop(a, b, k) {
  let xC = (1-k)*a[0] + k*b[0];
  let yC = (1-k)*a[1] + k*b[1];
  return [xC, yC];
}

Post Anterior
Post Seguinte